MGSurvE (MGSurvE: Mosquito Gene SurveillancE) is a software package created to optimize the distribution of mosquito traps in complex heterogeneous landscapes.
Model Description
Interest in use of genetic constructs to eliminate mosquito-borne diseases has grown over the latest years. Solid steps towards the creation of viable CRISPR/Cas9 genetic drives that allow us to tackle diseases such as malaria, dengue and Zika; have steadily taken place. As we move towards field trials the need to develop tools that allow us to make the most of our surveillance resources has been more pressing.
To this end, we have developed MGSurvE (Mosquito Gene SurveillancE), an open-source python framework that allows the characterization of mosquito landscapes and the optimization of traps’ placements to achieve the quickest detection of mutations in field trials. A key feature of our package is that it can take into account fundamental characteristics of mosquito movement, such as: attractiveness to resources, differences in male/female movement, resource-based attractiveness to traps, immovable traps, amongst others.
Migration Matrix
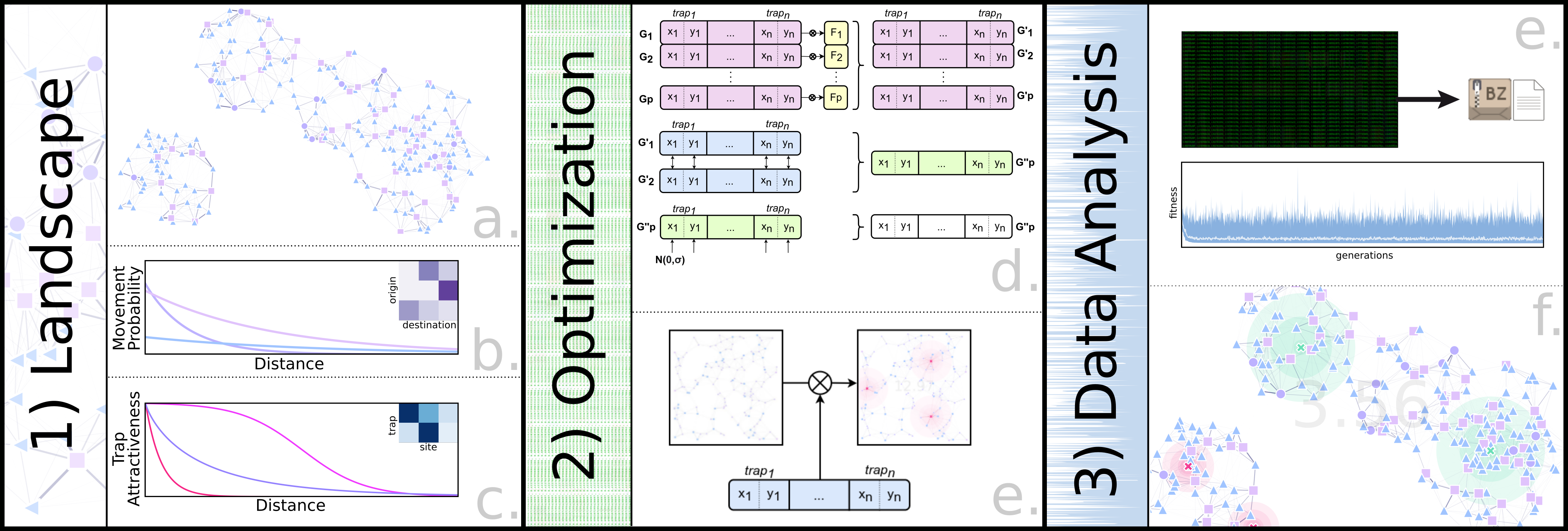
As it was the case for MGDrivE, the movement of mosquitos is modelled as a network of connected sites. In most cases, calculating the migration probability between sites is done with a kernel that is a function of the distance between sites \(\kappa\), and some biological parameters \(\rho\). This time, however, there is an additional masking parameter \(\lambda\) that varies depending on the probability of the individual moving from the point type of the source to the destination site.
\[\alpha(s_i\to s_j)= \kappa(D(s_i\to s_j), \rho_{bio}) * \lambda(\hat{s}_i, \hat{s}_j) * \theta_{j}\]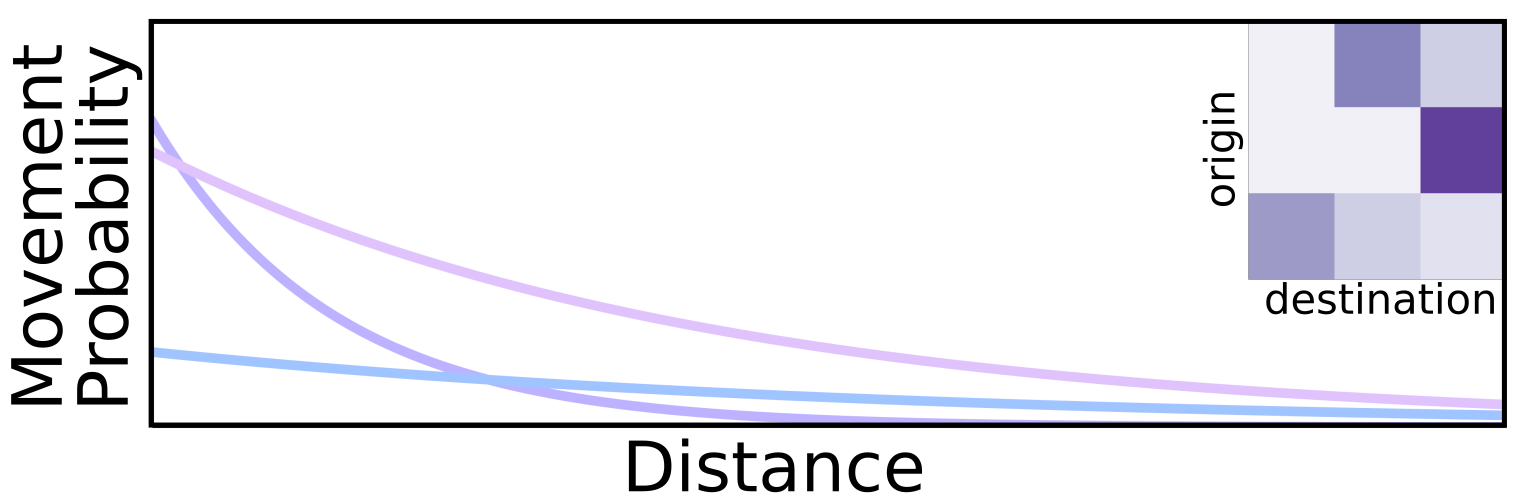
Repeating this process for each point pair, and normalizing the resulting matrix gives us our migration matrix \(\tau\):
\[\tau_{\{s_n,s_n\}} = \begin{Vmatrix} \alpha({s_1\to s_1}) & \alpha({s_1\to s_2}) & ... & \alpha({s_1\to s_{n-1}}) & \alpha({s_1\to s_n}) \\ \alpha({s_2\to s_1}) & \alpha({s_2\to s_2}) & ... & \alpha({s_2\to s_{n-1}}) & \alpha({s_2\to s_n}) \\ \vdots & & \ddots & & \vdots \\ \alpha({s_{n-1}\to s_1}) & \alpha({s_{n-1}\to s_2}) & ... & \alpha({s_{n-1}\to s_{n-1}}) & \alpha({s_{n-1}\to s_n}) \\ \alpha({s_n\to s_1}) & \alpha({s_n\to s_2}) & ... & \alpha({s_n\to s_{n-1}}) & \alpha({s_n\to s_n}) \end{Vmatrix}\]Migration With Traps
Now, to add traps into the migration equations, we calculate the probability of a mosquito falling into a trap with a trap attractiveness kernel \(\eta\); but this time, as mosquitos can’t escape the traps, and must remain in the same trap for the rest of the simulation, we have three different sections of the matrix:
\[\begin{align*} \delta(s_i\to t_j) &= \hat{\eta}(D(s_i\to t_j), \hat{\rho}_{trap}) * \phi(\hat{s_i}, \hat{t_j}) &\Rightarrow \nu_{\{s_n,t_n\}}\\ \delta(t_i\to s_j || t_i\to t_j |_{i\neq j}) &= 0 &\Rightarrow 0_{\{t_n,s_n\}}\\ \delta(t_i\to t_i) &= 1 &\Rightarrow I_{\{t_n,t_n\}} \end{align*}\]
To put these new sections together with the original migration matrix \(\tau\), we assemble the following block matrix \(\chi\):
\[\chi_{\{s_n+t_n, s_n+t_n\}} = \begin{Vmatrix} \tau_{\{s_n,s_n\}} & \nu_{\{s_n,t_n\}} \\ 0_{\{t_n,s_n\}} & I_{\{t_n,t_n\}} \end{Vmatrix}\]Fitness Function
For the optimization function to work, we need a fitness function (or cost function). In the gene drive context, we’d like to minimize the time it takes for detection of an undesired transgene. To calculate this, I decided to use the Markov fundamental matrix:
\[F_{\{s_n,s_n\}}=(I_{\{s_n,s_n\}}-\chi[\tau_{\{s_n,s_n\}}])^{-1}\]which gives us the number of timesteps it takes for a mosquito to fall into a trap from any initial point in the landscape. Now, to summarize this information into a metric, we can calculate the average maximum time from each one of these sites:
\[\begin{align*} \varphi_{\{s_n\}} &=Max^{j}(F_{\{s_n,s_n\}}(i, j))\\ \phi &= Mean(\varphi_{\{s_n\}}) \end{align*}\]Although other combinations could be used too (average of averages, medians, etcetera).


Code and Availability
Most of the package revolves around a landscape object exchanging information with the DEAP package. We are providing interfaces to do the calculations or provide overriding values (or functions) with demos and thorough documentation.
MGSurvE can be installed in its current development state from pypi. For more information please have a look at our documentation!