MGDrivE

A simulation framework for gene drive releases in spatially explicit mosquito populations, and its application to mosquito borne diseases control


IDDconf 2018
Héctor M. Sánchez C., Jared Bennett*, Sean L. Wu*, John M. Marshall
Contact: sanchez.hmsc@berkeley.edu Website: https://marshalllab.github.io/MGDrivE/

[Press the spacebar to move through the slides]

Agenda


1. Background [3 minutes]
2. The Model [3 minutes]
3. Application [5 minutes]
4. Closing Remarks [1 minutes]
5. Questions [3 minutes]

1. Background


A. Diseases
B. Gene-Drive Approaches
C. Hurdles to Overcome

1A. Diseases

1B. Gene-Drive Approaches



1C. Hurdles to Overcome

(from a modelling perspective)

2. MGDrivE


A. Modules
B. Tensor Equations
C. Demo

2A. Modules


2B. Tensor Equations


1) Genetic Inheritance

$$ \begin{align*} \overline{O(T_x)} = & \sum_{j=1}^{n} \Bigg( \bigg( (\beta*\overline{s} * \overline{ \overline{Af_{[t-T_x]}}}) * \overline{\overline{\overline{Ih}}} \bigg) * \Lambda \Bigg)^{\top}_{ij}\\ \end{align*}$$


2) Migration

$$ \begin{align*} \overline{Am_{(t)}^{i}}= &\sum{\overline{A_{m}^j} \otimes \overline{\overline{\tau m_{[t-1]}}}} \\ \overline{\overline{Af_{(t)}^{i}}}= &\sum{\overline{\overline{A_{f}^j}} \otimes \overline{\overline{\tau f_{[t-1]}}}} \end{align*} $$


3) Life History

$$ \begin{align*} \overline{L_{[t]}}= &\overline{L_{[t-1]}} * (1-\mu_{l}) * F(\overline{L_{[t-1]})} +\overline{O(T_e)}* \theta_{e} - \overline{O(T_e+T_l)} * \theta_{e} * D(\theta_l,0)\\ \overline{E^{'}}=& \overline{O(T_e+T_l+T_p)} * \bigg(\overline{\xi_m} * (\theta_{e} * \theta_{p}) * (1-\mu_{ad}) * D(\theta_l,T_p) \bigg)\\ \overline{Am_{[t]}}=& \overline{Am_{[t-1]}} * (1-\mu_{ad})*\overline{\omega_m} + (1-\overline{\phi}) * \overline{E^{'}} + \overline{\nu m_{[t-1]}}\\ \overline{\overline{Af_{[t]}}}=& \overline{\overline{Af_{[t-1]}}} * (1-\mu_{ad}) * \overline{\omega_f} + \bigg( \overline{\phi} * \overline{E^{'}}+\overline{\nu f_{[t-1]}}\bigg)^{\top} * \bigg( \frac{\overline{\eta}*\overline{Am_{[t-1]}}}{\sum{\overline{Am_{[t-1]}}}} \bigg)\\ \end{align*} $$


2C. Demo


3. Application


A. Drive: Threshold-Dependent Systems
B. Geography: Yorkeys Knob
C. Experiments: Factorial Sweeps
D. Results: Fixation Response Surfaces
E. Results: Remediation Response Surfaces

3A. Threshold-Dependent Systems


3B. Yorkeys Knob


3C. Experimental Setup


  • Time: 3 years
  • Households: 943
  • Household population: 15 mosquitos (around 14k total)
  • Release size proportion: 20 mosquitos
  • Releases location selection scheme: randomly uniform
  • Gene Drives: Reciprocal Translocations and Threshold Dependent Underdominance
  • Releases number: 0 to 20
  • Releases coverage: 0% to 100%
  • Outcome: Fixation/Dilution

3D. Fixation Response Surface

Reciprocal Translocations


3D. Fixation Response Surface

Threshold Dependent Underdominance


3D. Fixation Response Surface

Translocations VS Threshold Dependent Underdominance


       

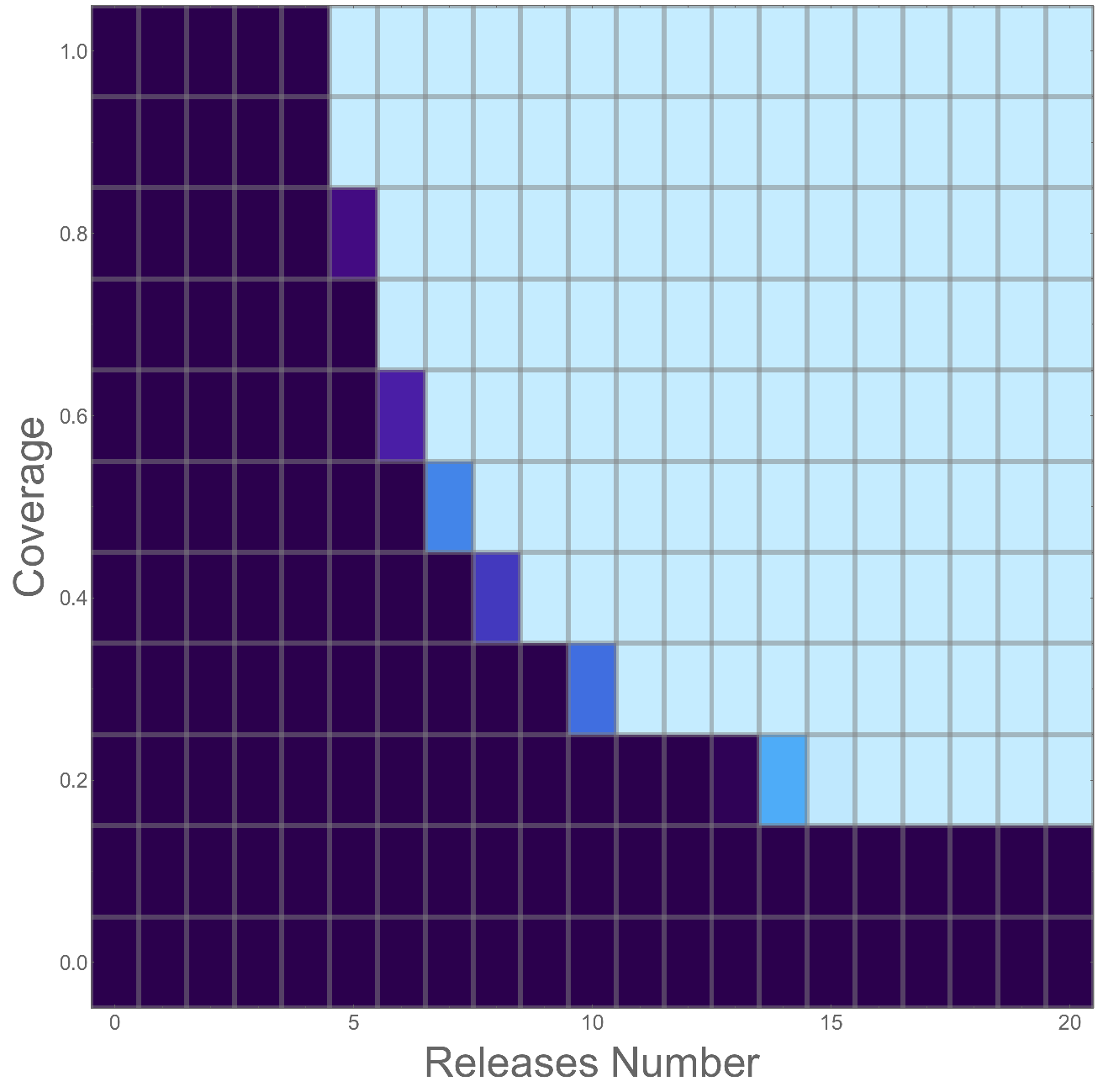
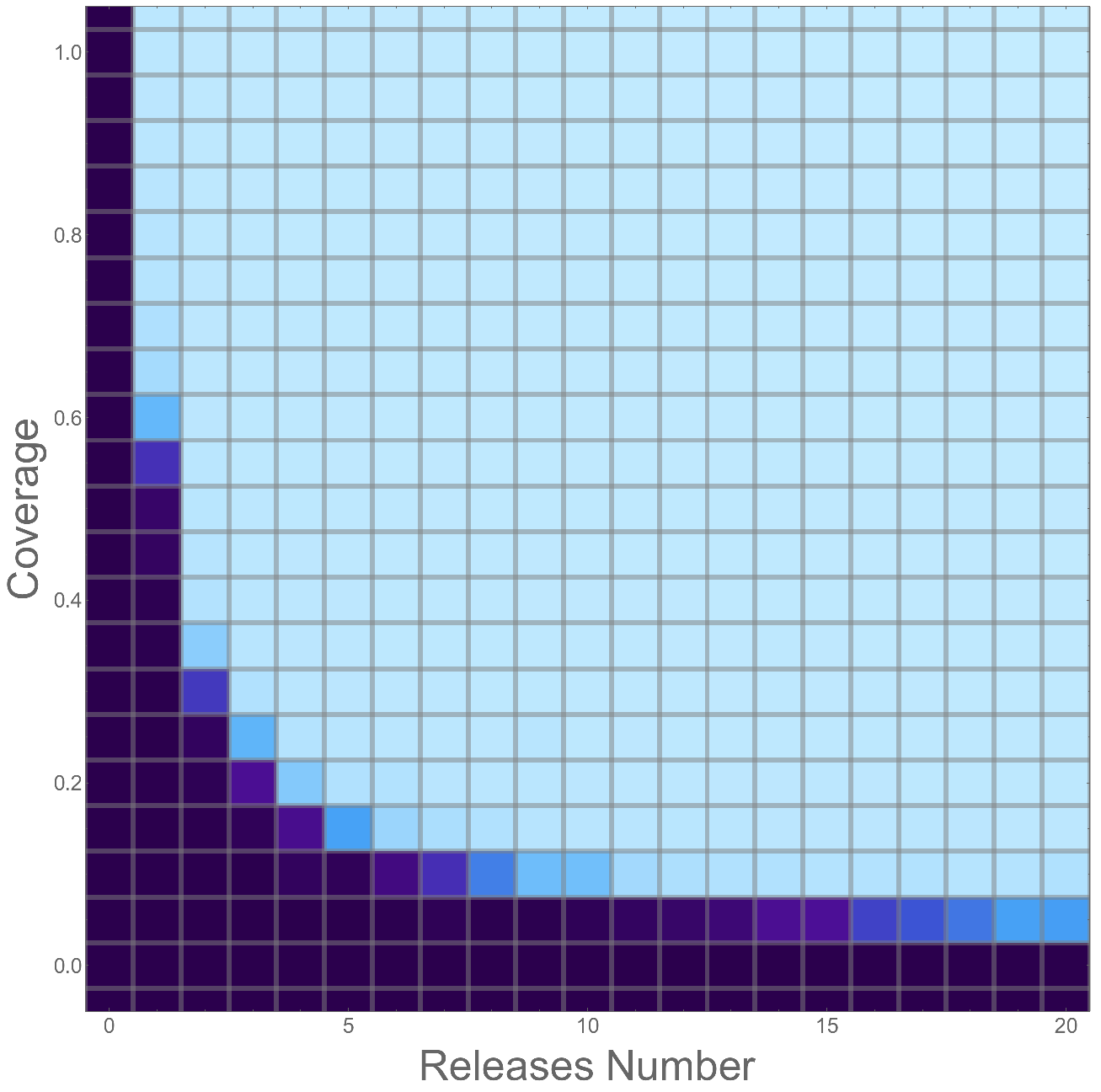
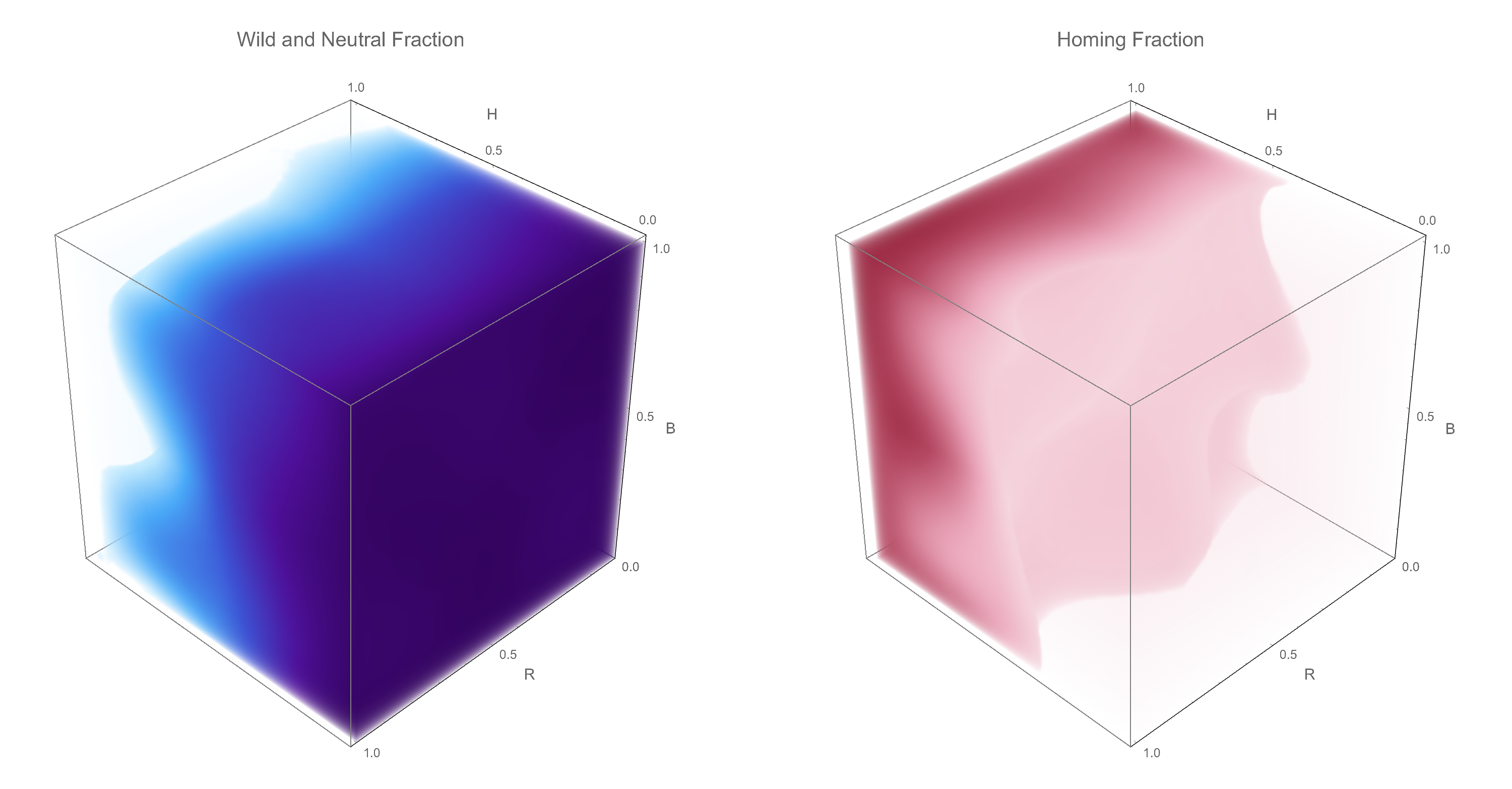
3E. Remediation Response Surface

Threshold Dependent Underdominance


4. Closing Remarks


A. Conclusions and Future Work
B. The Team

4A. Conclusions and Future Work


4B. The Team


Developed in: John Marshall's Lab by



Lead: Héctor M. Sánchez C.
Core Dev: Sean L. Wu, Jared Bennett
Environmental Factors: Tomás León
Releases Optimization: Valeri Vasquez
Spatial Analysis: Biyonka Liang, Sarafina Smith, Sabrina Wong
Movement Kernels: Partow Imani
Auxiliary Dev: Chase Violet


                                                                                


Questions